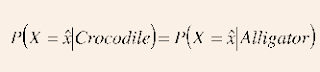BAYESIAN RISK ANALYSIS DATA

Nama Kelompok :

1. Amin Pujo Sakti (20112710)

2. Fajar Yudhi Purnomo (22112733)

3. M Riyan Nur Fatah (25112074)

4. Niko Santoso (25112321)

UNIVERSITAS GUNADARMA

FAKULTAS ILMU KOMPUTER

2012/2013

Kata Pengantar

Puji dan syukur kami panjatkan ke Hadirat Tuhan Yang Maha Esa, karena berkat limpahan Rahmat dan Karunia-Nya sehingga kami dapat menyusun buku ini dengan baik, serta tepat pada waktunya. Dalam buku ini kami akan membahas mengenai “Bayesian Risk Analys”

Buku ini telah dibuat dengan berbagai observasi, pencarian materim dan beberapa bantuan dari berbagai pihak untuk membantu menyelesaikan tantangan dan hambatan selama mengerjakan makalah ini. Oleh karena itu, kami mengucapkan terimak kasih yang sebesar besarnya kepada semua pihak yang telah membantu dalam penyusunan buku ini.

Kami menyadari bahwa masih banyak kekurangan yang mendasar pada buku ini. Oleh karena itu kami mengundang pembaca untuk memberikan saran serta kritik yang dapat membangun kami. Kritik konstruktif dari pembaca sangat kami harapkan untuk penyempurnaan buku selanjutnya.

Akhir kata semoga buku ini dapat memberikan manfaat terhadap kita semua.

Jakarta, Desember 2013

Penulis

Daftar Isi

Kata Pengantar

Daftar Isi

Bab 1

1.1 Latar Belakang

1.2 Tujuan Pembahasan

1.3 Metode Penyelesaian

Bab 2

2.1 Data Mining

2.2 Klasifikasi

2.3 Naive Bayesian Filtering

2.4 Teorama Bayes

Bab 3

3.1 Perangkat Keras

3.2 Perangkat Lunak

3.3 Pengujian

3.4 Pengujian Perangkat Lunak

3.5 Analisa Performansi Perangkat Lunak

Bab 4

4.1 Kasus/contoh pemanfaatan pada konsep

Bab 1

1.1 Latar Belakang 

Electronic mail (email) merupakan media komunikasi di internet seperti untuk berdiskusi (maillist), transfer informasi berupa file (mail attachment) bahkan dapat digunakan untuk media iklan suatu perusahaan atau produk tertentu. Mengingat fasilitas email yang murah dan kemudahan untuk mengirimkan ke berapapun jumlah penerimanya maka beberapa pihak tertentu memanfaatkannya dengan mengirimkan email berisi promosi produk atau jasa, pornografi, virus, dan content-content yang tidak penting ke ribuan pengguna email. Email-email inilah yang biasanya disebut dengan spam mail. 

Dampak buruk yang paling utama dari adanya spam mail adalah terbuangnya waktu dengan percuma untuk menghapus spam mail dari inbox satu persatu. Meskipun berbagai perangkat lunak email filtering banyak tersedia, namun masalah spam mail juga semakin berkembang. Oleh karena itu pada tugas akhir mata kuliah Sistem Keamanan lanjut ini, penulis mencoba menjelaskan email filtering untuk mengotomatisasikan proses pemilahan spam mail dan legitimate mail (bukan spam mail).

Salah satu metode email filtering yang paling populer yaitu naive bayesian filtering. Metode ini memanfaatkan teorema probabilitas yaitu teorema bayes dan fungsionalitas data mining yaitu klasifikasi naive bayesian. Kelebihan naive bayesian filtering diantaranya adalah tingkat akurasi yang tinggi dan error rate yang minimum. Hal inilah yang melatarbelakangi penulis untuk menjelaskan metode ini.

1.2 Tujuan Pembahasan 

Tujuan ingin dicapai dari tugas akhir ini adalah : Mengerti penggunaan dan cara kerja klasifikasi naive bayesian untuk membangun email filtering dan mengukur kinerja email filtering tersebut yaitu akurasi, skalabilitas dan robustnestnya.

1.3 Metode Penyelesaian 

Masalah Metode yang akan digunakan untuk menyelesaikan tugas akhir ini adalah : Studi Literatur Mempelajari literatur-literatur tentang email, teknik-teknik email filtering, konsep dan teknik data mining khususnya klasifikasi naive bayesian. 

Bab 2

DASAR TEORI

2.1 Data Mining 

Data mining atau Knowledge Discovery in Database (KDD) adalah ekstraksi informasi-informasi penting atau knowledge dari basis data yang besar. Data mining menspesifikasikan pola-pola yang ditemukan pada kumpulan data tersebut sehingga data yang telah ada itu lebih bermanfaat dalam kehidupan nyata. Fungsionalitas yang ada pada data mining antara lain Karakterisasi dan Diskriminasi, Asosiasi, Klasifikasi dan Prediksi, Analisa Cluster dan Analisa Outlier.

2.2 Klasifikasi 

Klasifikasi adalah proses pencarian sekumpulan model atau fungsi yang menggambarkan dan membedakan kelas data dengan tujuan agar model tersebut dapat digunakan untuk memprediksi kelas dari suatu obyek yang belum diketahui kelasnya.

Klasifikasi memiliki dua proses yaitu membangun model klasifikasi dari sekumpulan kelas data yang sudah didefinisikan sebelumnya (training data set) dan menggunakan model tersebut untuk klasifikasi tes data serta mengukur akurasi dari model. Model klasifikasi dapat disajikan dalam berbagai macam model klasifikasi seperti decision trees, Bayesian classification, k-nearest-neighbourhood classifier, neural network, classification (IF-THEN) rule, dll. Klasifikasi dapat dimanfaatkan dalam berbagai aplikasi seperti diagnosa medis, selective marketing, pengajuan kredit perbankan, dan email.

Eletronic Mail Eletronic mail atau lebih sering kita kenal dengan singkatan email merupakan salah satu layanan internet yang paling banyak digunakan. Email adalah media komunikasi yang murah, cepat dan mudah penggunaannya. Format email terdiri dari sebuah envelope, beberapa field header, sebuah blank line dan body. Email memiliki sifat data berupa teks yang semi terstruktur dan memiliki dimensi yang tinggi. Email Filtering Spam mail merupakan salah satu masalah yang sering sekali muncul dalam dunia internet khususnya untuk Iayanan email. Dari hari ke hari jumlah spam yang diterima oleh sebagian besar pengguna email semakin banyak dan sangat mengganggu. Pengguna email biasanya mengalami masalah (kerepotan) dalam menghapus spam mail satu persatu, sehingga salah satu cara untuk mengatasinya adalah dengan cara menggunakan email filtering yaitu mengotomasisasikan proses pemilahan antara email yang spam dan yang bukan spam. Beberapa metode yang dapat digunakan untuk email filtering antara lain Keyword filtering, Black listing dan White listing, Signature-Based Filtering, Naive Bayesian (Statistical) Filtering, Challenge-response filtering, Rule-based (heuristic) filtering.

Kebutuhan Email Filtering

• Binary Class, Email filtering hanya mengklasifikasikan email ke dalam kelas spam mail dan legitimate mail. 

• Prediksi, Email filtering mampu melakukan prediksi kelas dari suatu email. 

• Komputasi Mudah, Mengingat sifat data email yang memiliki dimensi tinggi maka dibutuhkan sebuah email filter yang mampu melakukan komputasi dengan mudah. 

• Learning, mampu melakukan learning dan email-email yang sudah ada sebelumnya. 

• Kinerja yang bagus, Memiliki akurasi yang tinggi, meminimalkan nilai false positive dan mentolerir nilai false negative yang cukup tinggi.

2.3 Naive Bayesian Filtering 

Naive bayesian filter merupakan metode terbaru yang digunakan untuk mendeteksi spam mail. Algoritma ini memanfaatkan teori probabilitas yang dikemukakan oleh ilmuwan Inggris Thomas Bayes, yaitu memprediksi probabilitas di masa depan berdasarkan pengalaman di masa sebelumnya. Dua kelompok peneliti, satu oleh Pantel dan Lin, dan yang lain oleh Microsoft Research memperkenalkan metode statistik bayesian ini pada teknologi anti spam filter. Tetapi yang membuat naive bayesian filtering ini popular adalah pendekatan yang dilakukan oleh Paul Graham. Banyak aplikasi menghubungkan antara atribut set dan variabel kelas yang non deterministic. Dengan kata lain, label kelas test record tidak dapat diprediksi dengan peristiwa tertentu meski atribut set identik dengan beberapa contoh training. Situasi ini makin meningkat karena noisy data atau kehadiran faktor confounding tertentu yang mempengaruhi klasifikasi tetapi tidak termasuk di dalam analisis. Sebagai contoh, perhatikan tugas memprediksi apakah seseorang beresiko terkena penyakit hati berdasarkan diet yang dilakukan dan olahraga teratur. Meski mempunyai pola makan sehat dan melakukan olahraga teratur, tetapi masih beresiko terkena penyakit hati karena faktor-faktor lain seperti keturunan, merokok, dan penyalahgunaan alkohol. Untuk menentukan apakah diet sehat dan olahraga teratur yang dilakukan seseorang adalah cukup menjadi subyek interpretasi, yang akan memperkenalkan ketidakpastian pada masalah pembelajaran.

2.4 Teorema Bayes

A. Penggunaan Teorema Bayes untuk Melakukan Klasifikasi 

Sebelum mendeskripsikan bagaimana teorema Bayes digunakan untuk klasifikasi, disusun masalah klasifikasi dari sudut pandang statistik. Jika melambangkan set atribut data dan melambangkan kelas variabel. Jika variabel kelas memiliki hubungan non deterministic dengan atribut, maka dapat diperlakukan dan sebagai variabel acak dan menangkap hubungan peluang menggunakan . Peluang bersyarat ini juga dikenal dengan posterior peluang untuk , dan sebaliknya peluang prior . Selama fase training, perlu mempelajari peluang posterior untuk seluruh kombinasi dan berdasar informasi yang diperoleh dari training data. Dengan mengetahui peluang ini, test record dapat diklasifikasikan dengan menemukan kelas yang memaksimalkan peluang posterior . Untuk mengilustrasikan pendekatan ini, perhatikan tugas memprediksi apakah seseorang akan gagal mengembalikan pinjamannya. 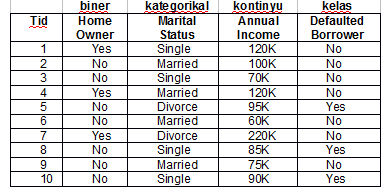Tabel 1 memperlihatkan training data dengan atribut : Home Owner, Marital Status, dan Annual Income. Peminjam yang gagal membayar diklasifikasikan sebagai seseorang yang membayar kembali pinjaman sebagai No. 

Tabel 1. Training set untuk masalah kegagalan pinjaman. 

Jika diberikan test record dengan atribut berikut : = (Home Owner = No, Marital Status = Married, Annual Income = $120K). Untuk mengklasifikasi record, perlu dihitung peluang posterior , berdasar informasi yang tersedia pada training data. Jika , maka record diklasifikasikan sebagai Yes, sebaliknya diklasifikasikan sebagai No. 

Untuk mengestimasi peluang posterior secara akurat untuk setiap kombinasi label kelas yang mungkin dan nilai atribut adalah masalah sulit karena membutuhkan training set sangat besar, meski untuk jumlah moderate atribut. Teorema Bayes bermanfaat karena menyediakan pernyataan istilah peluang posterior dari peluang prior , peluang kelas bersyarat dan bukti : 

Ketika membandingkan peluang posterior untuk nilai berbeda, istilah dominator, , selalu tetap, sehingga dapat diabailan. Peluang prior dapat dengan mudah diestimasi dari training set dengan menghitung pecahan training record yang dimiliki tiap kelas. Untuk mengestimasi peluang kelas bersyarat , dihadirkan dua implementasi metoda klasifikasi Bayesian.

B. Naive Bayes Classifier 

Naive bayes classifier mengestimasi peluang kelas bersyarat dengan mengasumsikan bahwa atribut adalah independen secara bersyarat yang diberikan dengan label kelas . Asumsi independen bersyarat dapat dinyatakan dalam bentuk berikut :

 

 dengan tiap set atribut terdiri dari atribut.

Independensi Bersyarat Sebelum menyelidiki lebih detail bagaimana naive bayes classifier bekerja, terlebih dahulu diuji notasi independensi bersyarat. Anggap , , dan melambangkan tiga set variabel acak. Variabel di dalam dikatakan independen secara bersyarat , yang diberikan , jika sesuai kondisi berikut. 

Contoh independensi bersyarat adalah hubungan panjang lengan manusia dengan kemampuan membacanya. Dapat diamati bahwa orang dengan lengan lebih panjang cenderung memiliki tingkat kemampuan membaca lebih tinggi. Hubungan ini dapat dijelaskan dengan kehadiran faktor confounding, yaitu usia. Seorang anak kecil cenderung memiliki lengan lebih pendek dan kemampuan membaca lebih sedikit dibanding orang dewasa. Jika usia seseorang ditetapkan, maka hubungan yang diamati antara panjang kengan dan kemampuan membaca akan hilang. Sehingga dapat disimpulkan bahwa panjang lengan dan kemampuan membaca adalah independen secara bersyarat ketika variabel usia ditetapkan. 

Independensi bersyarat antara dan juga dapat ditulis dalam bentuk serupa dengan Persamaan 2 : 

Persamaan 3 digunakan untuk memperoleh baris terakhir Persamaan.

Cara Kerja Naive Bayes Classifier Asumsi independen bersyarat, termasuk menghitung peluang bersyarat untuk setiap kombinasi , hanya memerlukan mengestimasi peluang bersyarat untuk tiap yang diberikan . pendekatan selanjutnya lebih praktis karena tidak mensyaratkan training set sangat besar untuk memperoleh estimasi peluang yang baik.

Untuk mengklasifikasi tes record, naive bayes classifier menghitung peluang posterior untuk tiap kelas : 

 adalah tetap untuk seluruh , cukup untuk memilih kelas yang memaksimalkan istilah numerator, . 

Mengestimasi Peluang Bersyarat untuk Atribut Kategorikal 

Atribut kategorikal, peluang bersyarat diestimasi menurut pecahan training instances pada kelas yang membuat nilai atribut khusus . Sebagai contoh, pada set training diberikan pada Tabel 1, tiga dari tujuh orang yang membayar pinjaman juga memiliki rumah. Sebagai hasil, peluang bersyarat untuk P(Home Owner = Yes|No) adalah 3/7. Dengan cara yang sama, peluang bersyarat untuk peminjam yang lalai adalah single diberikan oleh P(Marital Status = Single|Yes) = 2/3.

Mengestimasi Peluang Bersyarat untuk Atribut Kontinyu 

Ada dua cara untuk mengestimasi peluang kelas bersyarat untuk mengestimasi atribut kontinyu pada naive bayes classifiers. A. Mendiskritisasi tiap atribut kontinyu dan kemudian mengganti nilai atribut kontinyu dengan interval diskrit yang bersesuaian. Pendekatan ini mengubah atribut kontinyu ke dalam atribut ordinal. Peluang bersyarat diestimasi dengan menghitung pecahan training record yang dimiliki kelas yang berada di dalam interval yang bersesuaian untuk . Kesalahan estimasi tergantung pada strategi mendiskritisasi, sebagaimana halnya dengan jumlah interval diskrit. Jika jumlah interval terlalu besar, ada terlalu sedikit training record pada tiap interval untuk menyediakan estimasi yang reliable (dapat dipercaya) untuk . Di sisi lain, jika jumlah interval terlalu kecil, maka beberapa interval dapat aggregate records dari kelas berbeda dan batas keputusan yang benar dapat hilang. B. Diasumsikan bentuk tertentu distribusi peluang untuk variabel kontinyu dan mengestimasi parameter distribusi menggunakan training data. Distribusi Gaussian sering dipilih untuk merepresentasikan peluang kelas bersyaarat untuk atribut kontinyu. Distribusi dikarakterisasi dengan dua parameter yaitu mean, , dan varian, . Untuk tiap kelas , peluang kelas bersyarat untuk atribut adalah :

Parameter dapat diestimasi berdasarkan sampel mean untuk seluruh training record yang dimiliki kelas . Dengan cara sama, dapat diestimasi dari sampel varian training record tersebut. Sebagai contoh, dipertimbangkan atribut pendapatan tahunan yang ditunjukkan Tabel 1. Sampel mean dan varian untuk atribut ini yang berkenaan dengan kelas No adalah : Diberikan test record dengan pendapatan kena pajak sebesar $120K, maka dapat dihitung peluang kelas bersyarat sebagai berikut. Interpretasi terdahulu dari peluang kelas bersyarat dapat menyesatkan. Persamaan 6 pada sisi kanan bersesuaian dengan fungsi densitas peluang, . Karena fungsi bernilai kontinyu, peluang bahwa variabel acak mengambil nilai tertentu adalah nol. Sebagai gantinya, dihitung peluang bersyarat bahwa berada pada beberapa interval, dan dengan adalah konstanta kecil :

Karena muncul sebagai faktor pengali tetap untuk tiap kelas, maka dibatalkan ketika dinormalisasi peluang posterior untuk. Oleh karena itu, Persamaan masih dapat diterapkan untuk pendekatan peluang kelas bersyarat. Contoh naive bayes classifier Perhatikan data set yang ditunjukkan Tabel 2 (a). Peluang kelas bersyarat dapat dihitung untuk pengkategorian tiap atribut, bersama dengan sampel mean dan varian untuk atribut kontinyu menggunakan metodologi yang dijelaskan pada bagian sebelumnya. Peluang ini diringkas pada Tabel 2 (b).

(a)

Tabel 2. Naive Bayes Classifier untuk masalah klasifikasi pinjaman. 

(b)

For Annual Income : If class = No : sample mean = 110 Sample variance = 2975 If class = Yes : sample mean = 90 Sample variance = 25 (b)

Untuk memprediksi label kelas test record X = (Home Owner = No, Marital Status = Married, Income = $120K), perlu menghitung peluang posterior dan . Mengingat dari diskusi sebelumnya bahwa peluang posterior ini dapat diestimasi dengan menghitung produk antara peluang prior dan peluang kelas bersyarat , yang bersesuaian dengan pembilang pada sisi kanan Persamaan 5.

Peluang prior tiap kelas dapat diestimasi dengan menghitung pecahan tiap training record yang dimiliki tiap kelas. Karena ada tiga record yang dimiliki kelas Yes dan tujuh record yang dimiliki kelas No, = 0.3 dan = 0.7. Menggunakan informasi yang disediakan pada Tabel 2 (b), peluang kelas besyarat dapat dihitung sebagai berikut.

= P(Home Owner=No|No) x P(Status=Married|No) x P(Annual Income=$120K|No) = 4/7 x 4/7 x 0.0072 = 0.0024.

= P(Home Owner=No|Yes) x P(Status=Married|Yes) x P(Annual Income=$120K|Yes) = 1 x 0 x 1.2 x 10-9 = 0.

Dengan menggabungkan, peluang posterior untuk kelas No adalah , dengan adalah istilah tetap. Menggunakan pendekatan yang sama, dapat ditunjukkan bahwa peluang posterior untuk kelas Yes adalah nol karena peluang kelas bersyarat adalah nol. Karena , maka record diklasifikasikan sebagai No.

Mengestimasi Peluang Bersyarat 

Contoh sebelumnya mengilustrasikan masalah potensial denga mengestimasi peluang posterior dari training data. Jika peluang kelas bersyarat untuk atribut adalah nol, maka keseluruhan peluang bersyarat untuk kelas hilang. Pendekatan mengestimasi peluang kelas bersyarat menggunakan tuple pecahan mengkin terlihat terlalu rapuh, khususnya jika ada training sample yang tersedia dan jumlah atribut besar.

Pada kasus lebih ekstrim, tidak dapat mengklasifikasikan beberapa test record. Sebagai contoh, jika P(Marital Status=Divorced|No) adalah nol menggantikan 1/7, maka record dengan set atribut X = (Home Owner=Yes, Marital Status=Divorced, Income=$120K) memiliki peluang kelas bersyarat = 3/7 x 0 x 0.0072 = 0. = 0 x 1/3 x 1.2 x 10-9 = 0.

Naive bayes classifier tidak dapat mengklasifikasikan record. Masalah ini dapat ditujukan dengan menggunakan pendekatan m-estimasi untuk mengestimasi peluang bersyarat 

Dengan adalah total jumlah instances dari kelas , adalah jumlah contoh training dari kelas yang menerima nilai , adalah parameter yang dikenal sebagai ukuran sampel ekivalen, dan adalah parameter yang dispesifikasi pengguna. Jika tidak tersedia training set (misalnya = 0), maka . Oleh karena itu, dapat dikenali sebagai peluang prior dari pengamatan nilai atribut bersama record dengan kelas . Ukuran sampel ekivalen menetapkan pertukaran antara peluang prior dan peluang yang diamati .

Pada contoh yang diberikan sebelumnya, peluang bersyarat P(Status=Married|Yes) = 0 karena tidak ada training record kelas yang memiliki nilai atribut tersebut. Menggunakan pendekatan m-estimasi dengan =3 dan =1/3, peluang bersyarat tidak lagi nol. P(Marital Status=Married|Yes) = (0 + 3 + 1/3)(3 + 3) = 1/6.

Jika diasumsikan =1/3 untuk setiap atribut kelas Yes dan =2/3 untuk seluruh atribut kelas No, maka = P(Home Owner=No|No) x P(Status=Married|No) x P(Annual Income=$120K|No) = 6/10 x 6/10 x 0.0072 = 0.0026.

= P(Home Owner=No|Yes) x P(Status=Married|Yes) x P(Annual Income=$120K|Yes) = 4/6 x 1/6 x 1.2 x 10-9 = 1.3 x 10-10.

Peluang posterior untuk kelas No adalah : , sementara peluang posterior untuk kelas Yes adalah . Meski keputusan klasifikasi tidak diubah, pendekatan m-estimasi umumnya menyediakan cara lebih robust (kokoh) untuk mengestimasi peluang ketika jumlah training sampel kecil. Karakteristik Naive Bayes Classifier Naive Bayes Classifier umumnya memiliki karakteristik sebagai berikut. • Kokoh untuh titik noise yang diisolasi seperti titik yang dirata-ratakan ketika mengestimasi peluang bersyarat data. Naive bayes classifier dapat menangani missing value dengan mengabaikan contoh selama pembuatan model dan klasifikasi. • Kokoh untuk atribut tidak relevan, jika adalah atribut yang tidak relevan, maka menjadi hampir didistribusikan seragam. Peluang kelas bersyarat untuk tidak berdampak pada keseluruhan perhitungan peluang posterior. • Atribut yang dihubungkan dapat menurunkan performance Naive bayes classifier karena asumsi independen bersyarat tidak lagi menangani atribut tersebut. Sebagai contoh, perhatikan peluang berikut. P(A = 0|Y = 0) = 0.4, P(A = 1|Y = 0) = 0.6, P(A = 0|Y = 1) = 0.6, P(A = 1|Y = 1) = 0.4, dengan adalah atribut biner dan adalah variabel kelas biner. Jika ada atribut biner lain yaitu yang secara tepat dihubungkan dengan ketika = 0, tetapi independen dengan ketika = 1. Sederhanaya, diasumsikan bahwa peluang kelas bersyarat untuk sama seperti . diberikan record dengan atribut = 0, B = 0, dapat dihitung peluang posterior sebagai berikut. . Jika , maka naive bayes classifier akan menugaskan record ke kelas 1. Bagaimanapun, yang benar adalah : karena dan dihubungkan secara tepat ketika = 0. Sebagai hasil, peluang posterior untuk = 0 adalah : . yang lebih besar dibanding untuk = 1. Record diklasifikasikan sebagai kelas 0.

C. Error Rate (Tingkat Kesalahan) Bayes 

Jika diketahui distribusi peluang yang benar yang mengatur . Metoda klasifikasi Bayesian menyediakan penentuan batas keputusan ideal untuk tugas klasifikasi, sebagimana diilustrasikan contoh berikut.

Perhatikan tugas mengidentifikasikan alligator dan crocodiles berdasarkan panjang masing-masing. Panjang rata-rata crocodile dewasa sekitar 15 kaki sedangkan panjang rata-rata alligator dewasa sekitar 12 kaki. Diasumsikan bahwa panjang mengikuti distribusi Gaussian dengan standar deviasi sama dengan 2 kaki, peluang kelas bersyarat dapat dinyatakan sebagai berikut.

Gambar 1 Perbandingan fungsi likelihood antara crocodile dan alligator

Gambar 1 menunjukkan perbandingan antara peluang kelas bersyarat untuk crocodile dan alligator. Diasumsikan bahwa peluang prior adalah sama, batas keputusan ideal diletakkan pada panjang yaitu

Menggunakan persamaan 9 didapat, 

yang dapat dipecahkan dengan hasil = 13.5. Batas keputusan untuk contoh ini diletakkan di tengah antara dua mean.

Ketika peluang prior berbeda, batas keputusan menggeser kelas dengan peluang prior lebih rendah. Selanjutnya, minimum error rate dapat dicapai dengan setiap classifier yang diberikan data juga dapat dihitung. Batas keputusan ideal pada contoh terdahulu mengklasifikasikan seluruh mahluk dengan panjang kurang dari x sebagai alligator dan yang kurang dari sebagai crocodile. Error rate classifier diberikan dengan menjumlahkan luas di bawah kurva peluang posterior untuk crocodile (dari panjang 0 hingga ) dan luas di bawah kurva peluang posterior untuk alligator (dari hingga )

Total error rate dikenal sebagai Bayes error rate.

D. Bayesian Belief Network (BBN) 

Asumsi independen bersyarat dibuat oleh Naive bayes classifier mungkin terlalu rapuh, khususnya untuk masalah klasifikasi dengan atribut yang dihubungkan dengan sesuatu. Bagian ini menghadirkan pendekatan lebih fleksibel untuk memodelkan peluang kelas bersyarat . Sebagai ganti mensyaratkan seluruh atribut untuk independen secara bersyarat dengan kelas yang diberikan, pendekatan ini menspesifikasi pasangan atribut yang independen secara bersyarat. Diskusi dimulai dengan merepresentasikan dan membangun model peluang tersebut, diikuti contoh bagaimana membuat inferences dari model.

Representasi Model

BBN menyediakan representasi grafis dari hubungan peluang bersama dengan set variabel acak. Ada dua unsur kunci Bayesian network : 

1. Directed acyclic graph (dag) mengencode hubungan dependen antar set variabel. 

2. Tabel peluang mengasosiasikan tiap node ke node orangtua selanjutnya.

Perhatikan tiga variabel acak, A, B, dan dengan A dan B variabel independen dan masing-masing memiliki pengaruh langsung pada variabel ketiga C. Hubungan antar variabel dapat diringkas ke dalam directed acyclic graph yang ditunjukkan Tabel 2 (a). Tiap node pada grafik merepresentasikan sebuah variabel, dan tiap panah menyatakan hubungan dependen antara pasangan variabel. Jika arah panah dari X ke Y , maka X adalah orangtua Y dan adalah anak X. Selanjutnya jika jalur diarahkan pada network dari X ke Z, maka X adalah ancestor Z, sedang Z adalah descendant X. Sebagai contoh, pada diagram yang ditunjukkan pada Tabel 2 (b), adalah D descendant D dan ancestor B. Baik B dan D juga non-descendant A. Properti penting Bayesian network dinyatakan sebagai berikut.

Properti 1 (independensi bersyarat). Node pada Bayesian network independen secara bersyarat dengan non descendant-nya, jika orangtuanya diketahui.

Pada diagram yang ditunjukkan pada Tabel 2 (b), A adalah independen bersyarat dari B dan D diberikan C karena node untuk B dan D adalah non descendant node . Asumsi independen bersyarat dibuat dengan naive bayesian classifier juga dapat direpresentasikan menggunakan bayesian network, seperti ditunjukkan Tabel 2 (c),

dengan adalah target kelas dan adalah atribut set.

Disamping kondisi independen bersyarat yang dikenakan dengan topologi network, tiap node juga diasosiasikan dengan tabel peluang. 

1. Jika node X tidak memiliki orangtua, maka tabel hanya berisi peluang prior P(X). 

2. jika node X hanya memiliki satu orangtua, Y, maka tabel berisi peluang bersyarat P(X|Y).

3. jika node memiliki banyak orangtua ,

maka tabel berisi peluang bersyarat . 

Gambar 3 Bayesian belief network untuk mendeteksi heart disease dan heartburn pada pasien.

Gambar 3 memperlihatkan contoh Bayesian network untuk memodelkan pasien heart disease atau masalah heartburn. Tiap variabel dalam diagram diasumsikan bernilai biner. Node orangtua untuk heart disease (HD) sesuai dengan faktor resiko yang dapat menyebabkan penyakit, seperti Exercise (E) dan Diet (D). Node anak untuk heart disease bersesuaian dengan simptom penyakit, seperti chest pain (CP) dan blood pressure (BP) tinggi. Sebagai contoh, diagram memperlihatkan bahwa heartburn (Hb) dapat dihasilkan dari diet tidak sehat dan mendorong chest pain.

Node dihubungkan dengan faktor resiko hanya berisi peluang prior, di mana node untuk heart disease, heartburn dan symptom yang bersesuaian berisi peluang kondisional. Untuk menghemat ruang, beberapa peluang dapat dihilangkan dari diagram. Peluang yang dihilangkan dapat ditemukan kembali dengan mencatat bahwa dan , dengan melambangkan outcome berlawanan dari . Sebagai contoh, peluang bersyarat P(Heart Disease = No|Exercise = No, Diet =Healthy) = 1 - P(Heart Disease = Yes|Exercise = No, Diet =Healthy) = 1 – 0.55 = 0.45.

Pembuatan Model 

Pembuatan model di dalam Bayesian network melibatkan dua langkah berikut. 1. Membuat struktur network. 2. Mengestimasi nilai peluang di dalam tabel yang dihubungkan dengan tiap node. 3. Topologi network dapat diperoleh dengan mengencode knowledge (pengetahuan) subyektif dari expert domain. 

Algoritma berikut menghadirkan prosedur sistematis untuk menginduksi topologi Bayesian network.

Algoritma untuk menggenerate topologi Bayesian network. 

1. Let melambangkan total order variabel. 

2. For sampai do 

3. Let melambangkan variabel order tertinggi ke- di dalam . 

4. Let melambangkan set variabel terdahulu . 

5. Pindahkan variabel dari yang tidak mempengaruhi (menggunakan pengetahuan prior) 

6. Buat panah antara dan variabel yang tersisa di dalam . 

7. End for.

Algoritma tersebut menjamin topologi tidak berisi siklus apapun. Buktinya cukup jelas. Jika terdapat siklus, maka paling kurang satu panah menghubungkan urutan node tertinggi ke urutan node terendah. Karena algoritma mencegah setiap panah menghubungkan urutan node terendah ke urutan node tertinggi, tidak ada siklus di alam topologi.

Meskipun demikian, topologi network dapat berubah jika diterapkan skema untuk variabel. Beberapa topologi dapat inferior karena menginduksi banyak panah yang menghubungkan antara pasangan node berbeda. Pada prinsipnya, dapat diuji seluruh kemungkinan pengurutan untuk menentukan topologi yang paling tepat, sebuah tugas yang mahal secara perhitungan. Pendekatan alternatif untuk membagi variabel ke dalam beberapa variabel sebab akibat dan kemudian panah dari tiap variabel kausal (sebab) ke variabel akibat yang sesuai. Pendekatan ini memudahkan tugas untuk membangun struktur Bayesian network.

Ketika topologi yang tepat telah ditemukan, tabel peluang diasosiasikan dengan tiap node ditentukan. Mengestimasi peluang tersebut dapat dilakukan secara langsung dan sama dengan pendekatan yang digunakan oleh naive bayes classifier.

Karakteristik BBN 

Beberapa karakteristik umum metoda BBN sebagai berikut. 

1. BBN menyediakan pendekatan untuk menangkap pengetahuan sebelumnya (prior knowledge) dari domain tertentu menggunakan pemodelan grafis. Network juga dapat digunakan untuk mengenkode dependensi kausal antar variabel. 

2. Membangun network dapat menghabiskan waktu dan memerlukan usaha yang banyak. Bagaimanapun, ketika struktur network telah ditentukan, menambahkan variabel baru dapat dilakukan secara langsung. 

3. Bayesian network sesuai untuk menangani data yang tidak lengkap. Instansiasi dengan atribut yang hilang dapat ditangani dengan menjumlahkan atau mengintegrasikan seluruh nilai atribut yang mungkin. 

4. Metoda cukup kokoh untuk model yang overfitting karena data dikombinasikan secara peluang dengan pengetahuan sebelumnya.

Klasifikasi Naive Bayes Pendekatan Paul Graham 

Naive Bayesian Filtering pendekatan Paul Graham memanfaatkan metode klasifikasi bayesian dengan dua asumsi dasar yaitu nilai atribut dari kelas yang didefinisikan independen dari nilai atribut yang lain dan prior probabilitas suatu email sebagai spam tidak diketahui. Asumsi pertama dikenal dengan sebutan naive bayesian. Naive bayesian filter pendekatan Paul Graham bekerja sebagai berikut : Diketahui database email C. Email di C kemudian diklasifikasikan terlebih dahulu ke dalam kelas spam dan kelas legitimate. Tiap email di masing - masing kelas ditokenisasi. Untuk tiap token x, dapat dihitung s(x, spam) dan S(x,legitimate) berturut - turut yaitu banyaknya email di database spam yang berisi token x dan banyaknya email di database legitimate yang berisi token x. Dengan diketahuinya token x dapat dihitung probabilitas suatu message M sebagai spam Berdasarkan aturan Bayesian maka probabilitas M sebagai spam: 

Persamaan 11 digunakan untuk menghitung probabilitas token untuk menghasilkan suatu database filter yang berisi token/kata beserta nilai probabilitasnya dan digunakan untuk mengidentifikasi email yang masuk sebagai spam atau legitimate. Suatu message tentunya memiliki lebih dari satu token/kata sehingga untuk mengetahui peluang suatu email sebagai spam dengan diketahui V(M) = (xi, Xz, Xs, ..., Xn} dilakukan perhitungan kombinasi probabilitasnya. Dengan asumsi naive yaitu token/kata di M saling independen maka probabilitas email: 

Untuk mengidentifikasi email sebagai spam atau legitimate ditentukan suatu nilai. Jika nilai probabilitas email, sebagai spam (hasil dari persamaan 12) ≥ maka email diklasifikasikan sebagai spam dan sebaliknya jika hasilnya < maka email diklasifikasikan sebagai legitimate.

Metoda Adhoc 

Metoda adhoc digunakan untuk memilih feature/token yaug paling menarik baik yang mengindikasikan spam maupun legitimate yaitu dengan cara untuk setiap token x yang muncul di data training, dihitung nilai | P(M is spam|x) - Vi \. Kemudian diambil sejumlah N token dengan nilai tertinggi untuk menghitung nilai probabilitas email sebagai spam. Paul Graham menyarankan nilai N sebanyak 15-20. Jika semua token diambil maka akan menghabiskan waktu komputasi dengan percuma untuk menghitung token yang kontribusinya minimal. Sedangkan jika token yang diambil terlalu sedikit, maka ada kemungkinan token yang signifikan namun tidak terpilih.

Mengapa Naive Bayesian Filtering? 

Naive bayesian filtering memiliki kelebihan dibandingkan dengan metoda filtering yang lain, diantaranya adalah: 

1. Bayesian filter memiliki komputasi yang mudah. 

2. Bayesian memeriksa email secara keseluruhan yaitu memeriksa token di database spam maupun legitimate. 

3. Bayesian filtering termasuk dalam supervised learning yaitu secara otomatis akan melakukan proses learning dari email yang masuk. 

4. Bayesian filtering cocok diterapkan di level aplikasi client/individual user. 

5. Bayesian filtering cocok diterapkan pada binary class yaitu klasifikasi ke dalam dua kelas. 

6. Metode ini multilingual dan internasional. Bayesian filtering menggenerate token dengan pengenalan karakter sehingga mampu diimplementasikan pada email dengan bahasa apapun. 

Bab 3

UJI COBA BAYESIAN FILTERING 

3.1 Perangkat Keras 

Email filtering diujicobakan pada sebuah personal komputer dengan konfigurasi sebagai berikut : 

• Processor Intel Pentium 4 dengan kecepatan 2,6 GHz. 

• RAM 512 MB

• Harddisk 40 GB.

  

Gambar : Processor, Ram, dan harddisk

3.2 Perangkat Lunak 

Implementasi email filtering dengan naive bayesian dibangun pada sistem operasi Microsoft Windows XP dengan menggunakan Delphi 7 dan untuk penyimpanan databasenya digunakan Microsoft Access 2000. Email filtering ini diimplementasikan pada Aplikasi email client Microsoft Outlook 2002.

3.3 Pengujian 

Tujuan pengujian fungsionalitas aplikasi ini adalah untuk menghitung berapa rata-rata training yang dilakukan per-email untuk mendapatkan keakuratan klasifikasi yang baik. Dan dari pengujian ini juga akan dianalisa kinerjanya yaitu dengan menghitung nilai akurasi, false positive dan false negative. Pengujian email filtering ini dilakukan pada sebuah account personal email paulgraham@hotmail.com. Mailbox ini berisi 94 legitimate mail dan 185 spam mail. Dengan data yang sama email filtering di implementasi dengan spesifikasi sebagai berikut: 

• Pengujian Pertama Jumlah data training 50 email dengan 20 legitimate mail dan 30 spam mail. 

• Pengujian Kedua Jumlah data training 150 email dengan 50 legitimate mail dan 100 spam mail. 

• Pengujian Ketiga Jumlah data training 270 email dengan 90 legitimate mail dan 180 spam mail.

Data testing untuk tiap pengujian sama yaitu sebanyak 50 email dengan 30 spam dan 20 legitimate. Pembagian jumlah data legitimate mail maupun spam mail ditentukan secara manual disesuaikan dengan ketersediaan data. Konstanta bayes yang digunakan : bias = 0.4, threshold = 0.9, jumlah token = 20.

3.4 Pengujian Perangkat Lunak 

• Pengujian Legitimate Mail 

• Pengujian Spam Mail 

• Pengujian Robustness Mail

3.5 Analisa Performansi Perangkat Lunak 

Setelah dilakukan pengujian dengan beberapa contoh email seperti diatas rata-rata email harus ditraining sebanyak 2-6 kali sebelum diklasifikasikan dengan benar. 

• Akurasi Pengujian Pertama : Jumlah data training 50 email, email filtering dapat mengklasiflkasikan 37 email dengan benar dan salah klasifikasi sebanyak 18 email sehingga nilai akurasinya (37/50)* 100% =74% Pengujian Kedua : Jumlah data training 150 email, email filtering dapat mengklasiflkasikan 43 email dengan benar dan salah klasifikasi sebanyak 7 email sehingga nilai akurasinya (43/150)* 100% =86% Pengujian Ketiga : Jumlah data training 270 email, email filtering dapat mengklasiflkasikan 46 email dengan benar dan salali klasifikasi sebanyak 4 email sehingga nilai akurasinya (46/270)* 100% =92% 

• False Positive Pengujian Pertama : Jumlah data training 50 email, terdapat 3 legitimate mail yang diklasifikasikan sebagai spam mail. Nilai false positivenya adalah (3/50)* 100%= 6% Pengujian Kedua : Jumlah data training 150 email, terdapat 3 legitimate mail yang diklasifikasikan sebagai spam mail. Nilai false positivenya adalah (3/50)* 100%= 6% Penguiian Ketiga : Jumlah data training 270 email, terdapat 1 legitimate mail yang diklasifikasikan sebagai spam mail. Nilai false positivenya adalah (1/50)* 100% =2% 

• False Negative Pengujian Pertama : Jumlah data training 50 email, terdapat 10 spam mail yang diklasifikasikan sebagai legitimate mail. Nilai false negativenya adalah (10/50)* 100%= 20% Pengujian Kedua : Jumlah data training 150 email, terdapat 4 spam mail yang diklasifikasikan sebagai legitimate mail. Nilai false negativenya adalah (4/50)*100%=8% Pengujian Ketiga : Jumlah data training 270 email, terdapat 3 spam mail yang diklasifikasikan sebagai legitimate mail. Nilai false negativenya adalah (3/50)* 100% =6% 

• Skalabilitas Email filtering mampu melakukan training dari jumlah data kecil hingga 270 email. Semakin besar jumlah data training maka nilai akurasinya semakin tinggi. Email filtering memiliki kinerja yang bagus untuk data dengan skala besar. 

• Robustness Email Filtering mampu menangani noise email yaitu email legitimate yang memiliki pola seperti spam mail dan sebaliknya. Meskipun untuk mendapatkan klasifikasi yang benar harus dilakukan training terlebih dahulu sebanyak 4-6 kali. 

• Waktu Pemrosesan Email filtering ini membutuhkan waktu 3.15 jam untuk melakukan training dengan data sebanyak 50 email, 6.23 jam untuk melakukan training dengan data sebanyak 150 email dan 9.6 jam untuk melakukan training dengan data sebanyak 270 email. Pada awal training waktu pemrosesan untuk menggenerate token pada sebuah email rata-rata selama 30 detik namun setelah jumlah email lebih dari 10 waktu pemrosesan sebuah email menjadi 65 menit. Sedangkan proses menggenerate bayes filter hanya membutuhkan waktu 15 menit. Pada saat testing, proses klasifikasi email membutuhkan waktu sekitar 0.5 detik hingga 8 menit. Sedangkan untuk proses learning sebuah email, dibutuhkan waktu selama 6 menit. Lamanya waktu pemrosesan disebabkan oleh banyaknya token yang digenerate pada training seiring dengan bertambahnya jumlah email yang digunakan. Sehingga proses pengupdate-an token, frekuensi dan probabilitas token membutuhkan waktu yang sangat lama. 

Bab 4

4.1 Kasus / contoh pemanfaatan pada konsep

Kasus 1 :

tidak ada informasi terdahulu Tanpa informasi sebelumnya, dapat ditentukan apakah sesorang memiliki heart disease dengan menghitung peluang prior P(HD=Yes) dan P(HD=No). Untuk menyederhanakan notasi, melambangkan nilai biner dari Exercise dan melambangkan nilai biner dari Diet.

= 0.25 x 0.7 x 0.25 + 0.45 x 0.7 x 0.75 + 0.55 x 0.3 x 0.25 + 0.75 x 0.3 x 0.75 = 0.49

Karena P(HD=no) = 1 - P(HD=yes)=0.51, orang tersebut besar kemungkinan tidak terkena penyakit tersebut.

Kasus 2 : 

tekanan darah tinggi Jika seseorang memiliki tekanan darah tinggi, dapat dilakukan diagnosa penyakit hati dengan membandingkan peluang posterior P(HD = Yes|BP=High) dengan P(HD = No|BP=High). Untuk melakukan ini, harus dihitung P(BP=High).

= 0.85 x 0.49 + 0.2 x 0.51 = 0.5185. dengan . Oleh karena itu, peluang posterior seseorang memiliki penyakit hati adalah :

. Dengan cara yang sama, P(HD = No|BP=High) = 1 – 0.8033 = 0.1967. Oleh karena itu, ketika seseorang memiliki tekanan darah tinggi, maka resiko terkena penyakit hati akan meningkat.

Kasus 3 : 

Tekanan darah tinggi, diet sehat dan olahraga teratur Jika diberitahu bahwa orang tersebut melakukan olahraga teratur dan makan dengan pola diet yang sehat. Bagaimana informasi baru mempengaruhi diagnosa? Dengan informasi baru tersebut, peluang posterior bahwa seseorang terkena penyakit hati adalah :

= 0.5862

sedang peluang bahwa seseorang tidak terkena penyakit hati adalah : P(HD=No|BP=High, D=Healthy, E=Yes) = 1 – 0.5862 = 0.4138.

Model tersebut selanjutnya menyatakan bahwa dengan pola makan sehat dan melakukan olahraga teratur akan mengurangi resiko penyakit hati. 

Bab 5

5.1 Kesimpulan

1. Klasifikasi naive bayesian pendekatan Paul Graham dapat digunakan dengan baik dalam aplikasi email filtering pada level client. 

2. Semakin banyak jumlah data yang digunakan untuk training maka semakin tinggi keakuratannya. 

3. Semakin sering dilakukan learning atau penambahan knowledge maka akan semakin cepat mendapatkan klasifikasi dengan benar. 

4. Email filtering dengan naive bayesian masih memiliki akurasi yang tinggi meskipun jumlah data trainingnya sedikit (270 email). 

5. Email filtering mampu menangani noise email dengan baik meskipun untuk mendapatkan akurasi dengan tepat harus dilakukan learning sebanyak minimal 4 kali. 

6. Sebuah email memiliki waktu prediksi minimal 0.5 detik (untuk email dengan isi teks yang pendek) dan maksimal 8 menit (untuk email dengan isi teks yang panjang dan banyak). 

7. Aplikasi ini memiliki waktu pemrosesan yang tinggi pada saat preprocessing dengan jumlah data yang semakin banyak dan pada saat melakukan learning. 

5.2 Saran

1. Aplikasi dapat dikembangkan lebih lanjut, misalnya dengan menentukan nilai variasi konstanta bayes secara otomatis untuk mendapatkan akurasi yang tinggi dengan berapapun jumlah data trainingnya. 

2. Aplikasi dapat dikembangkan lebih lanjut dengan melakukan analisa terhadap body email bertipe html atau mime dan attachment yang dianalisa dari contentnya. 

3. Aplikasi dapat disempurnakan untuk meminimalisir waktu pemrosesan pada saat learning seperti dengan menambahkan proses expired token yaitu menghapus token-token yang tidak lemah digunakan dalam klasifikasi sehingga jumlah token yang diupdate tidak terlalu banyak.